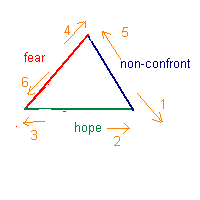
The vectors in the 'Terrible Triangle' are yielding a self-reinforcing system, in this case an 'expanding' triangle. This triangle is based on observation. There are countless other  'triangles' or 'triads' that can be observed.

For now, let's look at variations of the fear/hope/non-confront triad:
 
 
 

Triads can also be observed in all branches of physics and biology. The question arises therefore if these triads form instantiations of more basic 'law about laws'.   'Instantiation' here means a rule that has been formed according to an underlying more general rule.

The most basic set of rules, is often called an 'axiomatic system'. Such a system (a set of rules) cannot, by definition, be reduced to a system with less rules. This means, amongst other things, that its elements cannot be described in less stringent terms, and most importantly, no 'proof' can be established that the system is true because the enumeration of instances of an axiomatic system would be boundless task, a classic infinity problem.

However, an axiomatic system can be 'proven' incorrect if at least one instance of the set of rules can be found that does not follow the rules of the axiomatic system.

One of the earliest claims of the discovery of a 'basic system' can be attributed to the Chinese 'I-Ching'. It is often assumed that the I-Ching describes a 'binary system' and in a very restricted sense this is, of course, correct. But looking at the structure of formulations of rules within the text of the I-Ching, it becomes immediately obvious that, regarding establishment of rules, they really describe triads.

Another ancient triad system is the Indian 'guna' theory. While the I-Ching system does not 'explain' its triadic structure, the 'guna' theory is more explicit but still diffuse and not widely known and/or accepted.

In the Western Hemisphere, triads have been postulated by several philosophers, most notably Hegel. Ironically, as it is the case with the I-Ching, his triads are generally known as a 'dualistic' system, the 'dialectical process' that later found its way into politics via the theories of Feuerbach Marx,  Engels, et alii.

The most concise description yet has been done by a German-Argentinian philosopher with the name Anastasios Nordenholz. Since a description of the laws of the laws of this Universe can be called a 'Science about Science', he formed the appropriate name 'Scientologie' and summarized his insights 1934 in a book with the same name. A later revision appeared 1937.

Close to twenty years later, the same name was used to form the foundation of a Church. But that belongs, of course, into a completely different book !?!

What does this all have to with 'escaping from this Universe'?

Once the basic 'meta'-law is known,  relationships between any phenomena can be more easily found or even predicted. This knowledge can be rightfully called the 'ultimate leverage' in any toolbox of mental gadgets in philosophy or science.

Let's look at the properties of the left column in the table above:
 

• Every item describes a phenomenon that has to do with the degree with which an 'individuum' separates itself from the rest of the Universe.  In 'non-confront'  this separation is much larger than in 'affinity' or even 'attachment'.

Nordenholz called this leg of the 'meta'-triangle the 'First Axiom of Scientologie', or the 'Axiom of Individuation'.

• The middle column in above table shows how a Being 'specifies' what it perceives, or, from a different perspective, its perceived 'reality' or, from yet another angle, its 'knowledge'.

• The right column is the linking element in between 'individuation' and 'specification' and Nordenholz called this the third axiom of Scientologie, the 'Axiom of Mediation'. It is here where the 'action' is (literally).

Now, interestingly, two of the triads above appear in Hubbard's (applied) philosophy that he called 'Scientology', namely the ARC and the KRC triangles (examples 3 and 5). But, in a strange twist of fate, he didn't call them instantiations of the 'Axioms of Scientology'. Instead, he made up two long lists of statements and called those 'The Axioms Dianetics' and 'The Axioms of Scientology'. The number of items on these lists  is in the 100 range and, clearly,  his interpretation of the word 'axiom' is far away from the traditional philosophical or mathematical context. In especially, Hubbard's axioms do not form a 'minimal system', a prerequisite for the use of 'axioms' to begin with.

Gotamo (the 'Buddha') used the triad described in the 4th row in the table above. He integrated the triads that he used into a larger system of triads which he developped into the 'Arising depended upon a condition' sequence on one side and to the 'Eightfold Path' on the 'application' side.

There is much more to find out about these triads: for example, how the axioms are connected to the basic cycles of any process ('begin' - 'change' - 'end'), how they are interconnecting with each other, and what geometry would result from combinations of triads (hint, hint: the interconnections have to follow the axioms as well or else the axiomatic system would fail).

Last, not  least, and notably, ahem, there is the 'Sandorian System of Fractal Triads'.

In any case, looking at the meta-laws (or structure) of the Universe provides a veritable scientific way (in the correct sense of the word 'scientific') of research and discovery.

The results of its application are at times surprising and unexpected but always revealing and enlightening.

Enjoy your journey of discovery!